论文信息

Arxiv ID↗

幻觉翻译↗

Title:SpinQuant: LLM Quantization with Learned Rotations SpinQuant : 带有学成旋转的 LLM 量化

Part I: Foundation and Motivation

1. 当前研究目标与挑战

• 目标：将大型语言模型（LLMs）从 16 位浮点数 (FP16) 转换到 4 位整数 (INT4)，以大幅减少模型大小（$4\times$ 压缩）并提高推理速度。
• 挑战：LLMs 基于 Transformer 架构，其内部存在大量 异常值 (Outliers)，特别是经过 FFN 模块的非线性激活函数后。这些 Outliers 会导致量化精度急剧下降。
  • FFN (Feed-Forward Network)：负责对每个 Token 的特征进行非线性提炼，是模型中参数量最大的部分。
  • LayerNorm / RoPE：这些结构虽然帮助模型稳定训练（如 LayerNorm），但它们的输出分布依然可能产生 Outliers。

2. The Pre-SpinQuant Idea

为了解决 Outliers 问题，前人提出了一种思路：旋转平滑。

• 原理：Outliers 往往集中在特征向量的少数几个通道上。如果能对向量进行一次 空间旋转，这些 Outliers 的能量就会被分散（摊平）到所有通道上，使数据分布变得更像“高斯分布”或至少更均匀，从而更适合量化。
• 传统做法：之前的尝试（如 QuaRot）使用 随机 或 固定的 正交矩阵（如 Hadamard 矩阵）进行旋转。

3. The Insight

SpinQuant 通过实验发现了一个关键事实：

“不同的随机旋转矩阵会导致高达 13 个百分点的下游任务精度差异。”

这个发现表明，旋转矩阵的选择是至关重要的。 既然随机旋转的风险太大，一个自然的想法产生了：那么为什么不通过优化算法，学习 出一个能使量化误差最小的 最优旋转矩阵 $R$ 呢？

Part II: Core Method

SpinQuant 的核心是 在保持模型功能不变的前提下，优化数据分布。

1. Basic：Rotational Invariance 旋转不变性

对于 Transformer 中的任何线性层（矩阵乘法）$Y = X W$：

• $X$：输入激活值矩阵。
• $W$：权重矩阵。
• $R$：我们引入的 正交旋转矩阵。

我们同时对 $X$ 和 $W$ 进行变换：

1. 旋转激活值：$X' = X R$
2. 逆旋转权重：$W' = R^{-1} W$

将它们代入计算： $Y' = X' W' = (X R) (R^{-1} W) = X (R R^{-1}) W$

关键约束：为了保证 $Y' = Y$，我们要求 $R$ 必须是 正交矩阵，即 $R^{-1} = R^T$。 $\implies Y' = X (R R^T) W = X (I) W = X W = Y$

结论：在全精度下，新的 $Y'$ 严格等于 $Y$。这允许我们 离线 (Offline) 计算 $W' = R^T W$，用 $W'$ 替换原始 $W$，而不引入额外的推理开销。

2. Cayley SGD

由于 $R$ 必须满足 $R R^T = I$ 的 正交约束，我们不能使用传统的 SGD。

• 挑战：传统的 SGD 更新 $R \leftarrow R - \eta \nabla R$ 会使得 $R$ 失去正交性。
• 解决方案：使用 Cayley SGD（一种流形优化算法）。

Cayley SGD 的核心思想： 它通过 Cayley 变换，确保每一步梯度更新后，新的矩阵 $R'$ 仍然严格保持在 正交矩阵的空间（Stiefel 流形）内。

Simplified:

1. 计算梯度 $G = \nabla_R \mathcal{L}$。
2. 构造一个反对称矩阵 $Y$（满足 $Y^T = -Y$）： $Y \propto G R^T - R G^T$
3. 应用 Cayley 变换 进行更新： $R' = (I - \frac{\alpha}{2} Y)^{-1} (I + \frac{\alpha}{2} Y) R$
   • （其中 $\alpha$ 是学习率）。
   • 这个公式保证了 $R'$ 始终是正交的。

3. 目标函数 (Loss Function)

优化目标是最小化量化后模型的输出与全精度模型输出之间的误差： $\arg \min_{R} || \text{Logits}_{\text{FP16}} - \text{Logits}_{\text{Quant}}(R) ||_2$ 只需要使用少量校准数据，对 $R$ 进行数百步的微小优化即可。

Part III: Architecture & Deployment

SpinQuant 在 Transformer Pipeline 中设置了四种旋转矩阵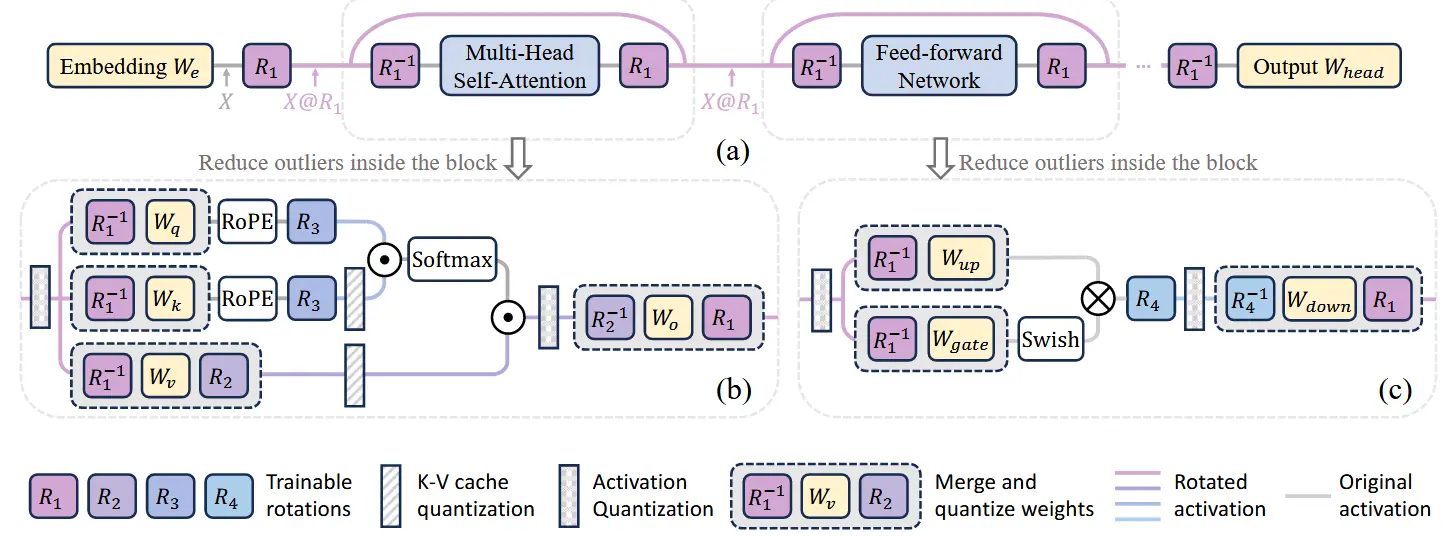$R_1 R_2 R_3 R_4$

1. 离线可吸收旋转 ($R_1, R_2$)

• 在推理时，模型无需执行 $R_1$ 或 $R_2$ 的乘法，因为它们的逆 $R^T$ 已经编码到了权重中。

2. 在线计算旋转 ($R_3, R_4$)

这些矩阵无法被融合，必须在运行时计算，但它们被强制约束为 Hadamard 矩阵，以实现高效计算。

Part IV: Results and Conclusion

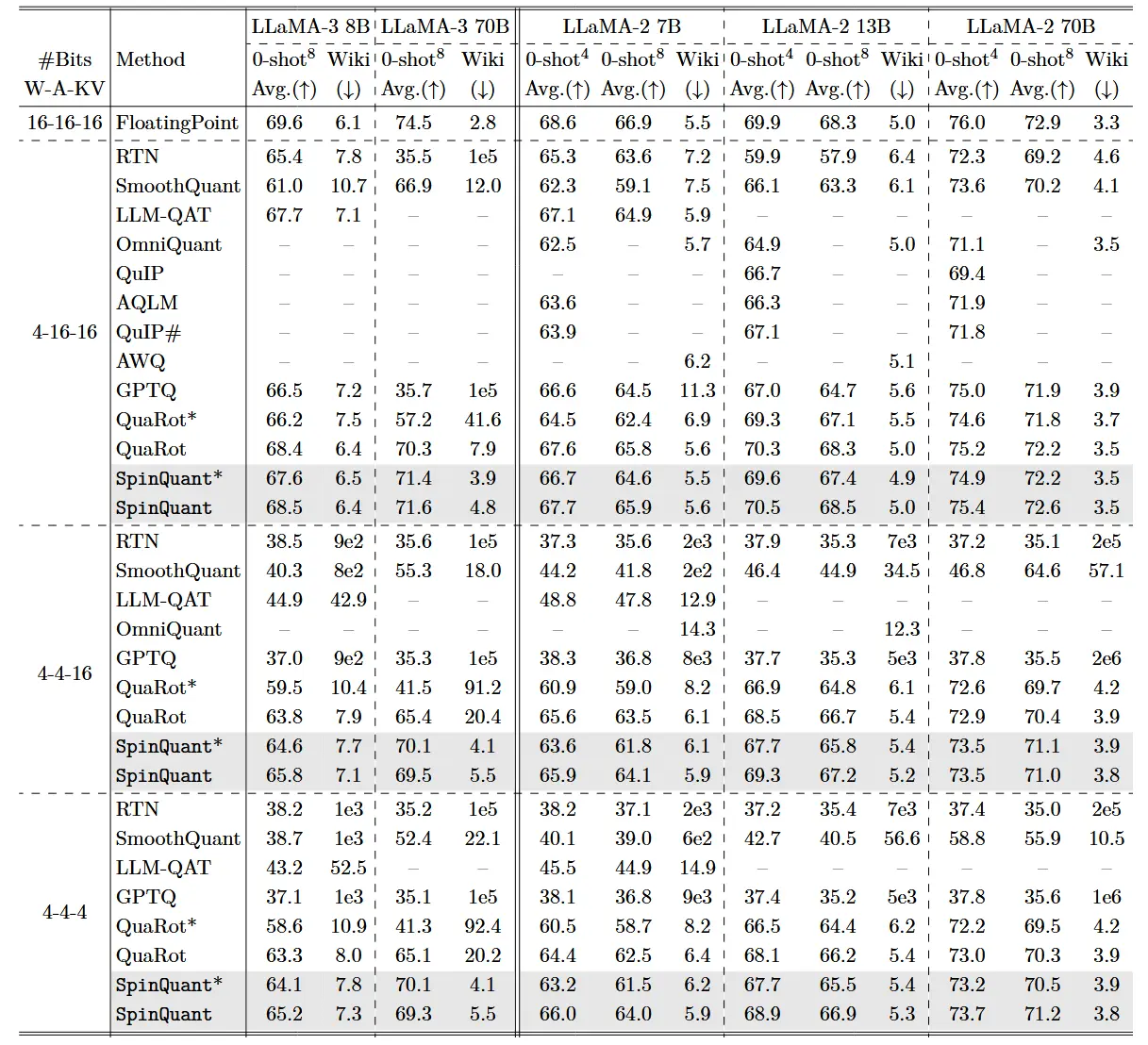
1. W4A4KV4 极限量化

• 在 LLaMA-2 7B 模型上，实现 权重、激活值、KV Cache 全部 4-bit 量化 (W4A4KV4)。
• 零样本推理任务的精度差距：仅 2.9 个百分点（与 FP16 相比）。
• baseline：
  • LLM-QAT：差距高达 22.0 个百分点。
  • SmoothQuant：差距高达 25.0 个百分点（在 A4 场景下失效）。
  • QuaRot：差距远大于 15 个百分点。

2. 结论

SpinQuant 将 流形优化 引入了 PTQ 领域。

• 突破：证明了通过学习最优旋转是实现 LLM 全链路 4-bit 极限量化的关键，效果远超硬编码规则（SmoothQuant）和随机方法（QuaRot）。

Thanks for reading!

Paper Reading Week3

Fri Nov 28 2025

1405 words · 6 minutes

Paper Reading PTQ

---

© lnscq | CC BY-NC-SA 4.0

Share

Share this article

X (Twitter) Telegram Reddit Facebook Email

Close

Close