Lecture 2 Imitation Learning
0.引言
在上一讲中,我们将强化学习形式化为一个清晰的优化问题:通过与环境的交互,学习一个策略,使其在期望意义下最大化累计奖励。从理论角度看,这一表述是完备且优雅的。然而,在真实系统中,这一范式往往直接遭遇实践层面的困难。
首先,环境交互的成本在许多任务中是不可忽略的。真实机器人、自动驾驶系统或面向用户的在线系统,都无法承受大规模、无约束的试错过程。其次,奖励函数在许多任务中并不容易被精确定义。人类通常能够判断“一个行为是否合理”,但将这种判断转化为稳定、可优化的标量信号本身就是一个困难的问题。
更进一步,在不少场景中,人类专家已经能够完成任务,并且已经积累了大量可供记录的行为数据。这自然引出了一个核心问题:在不显式构造奖励函数、也不依赖大规模环境交互的前提下,是否可以直接从专家行为中学习策略?
因此,我们引入了模仿学习(Imitation Learning)。
1.基本问题设定
模仿学习假设我们可以访问一组由专家策略生成的示范数据。这些数据通常以轨迹的形式给出,每条轨迹由状态序列及其对应的专家动作构成。形式化地,可以将数据集表示为
其中数据由某个未知但性能良好的专家策略 采样得到。
模仿学习的目标并不是推断环境动力学或奖励函数,而是直接学习一个参数化策略 ,使其在状态分布上尽可能复现专家的决策行为。从这一角度看,模仿学习的关注点不在于“什么是好的状态”,而在于“专家在这些状态下采取了什么样的行动”。
这一设定在形式上与监督学习高度相似,但其后果却截然不同。
2.模仿学习 Version 0:行为克隆
行为克隆(Behavior Cloning, BC)的最常见形式,是用监督学习拟合专家动作。若采用确定性策略,典型目标为平方损失回归:
这一写法在形式上简洁,但它隐含了一个非常强的建模偏置:在给定状态 时,模型被鼓励输出一个“单值”动作 。当专家行为在同一状态下近似唯一时,这种偏置并不明显;然而在实际数据中,专家往往并非单一来源,或存在等价可行的多种决策模式,于是问题就会显现。
3.为什么 回归会学到“均值”?
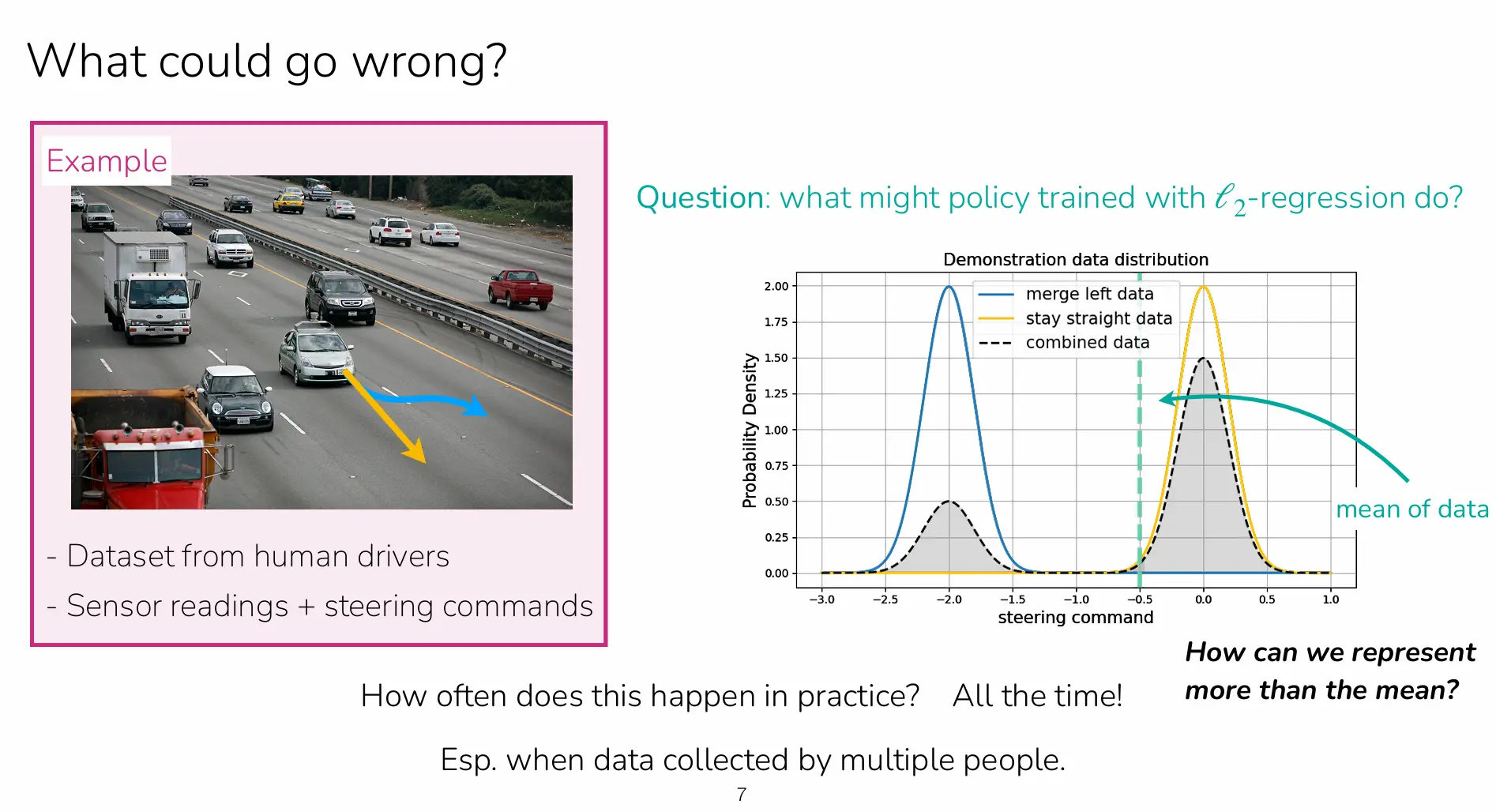
如果示范数据在某些状态上呈现多模态(例如一部分专家选择“并入左侧车道”,另一部分选择“保持/并入右侧”),那么用 损失训练的确定性政策会倾向输出条件均值。更具体的说,在固定 的条件下,最小化 的最优解满足:
这意味着:当数据分布在动作空间有两个峰时,均值往往落在“两个峰之间”的低概率区域。在驾驶这样的安全敏感任务里,这种折中动作会是灾难性的。
因此,我们可以认识到:模仿学习的挑战不一定来自网络不够大,而可能来自输出分布的表达能力不足。换句话说,“函数逼近能力”与“分布表达能力”是两件不同的事。
4.如何用神经网络表示动作分布
对于离散动作,举个例子,超级马里奥的上下左右操作。神经网路可以直接输出一个categorical分布的参数:
对于连续的动作,例如机器人每个关节的旋转角度、位姿估计,最常见的做法是让网络输出一组高斯分布参数。
这种单峰高斯分布参数化计算便利,但表达能力明显受限。因为即使网络参数再大, 仍然只是单峰型状态,很难在多模态的示范模型中对应复杂的条件分布。
5.生成模型视角
我们可以将模仿学习同生成模型的目标相联系。举个例子图像diffusion模型学习的目标是、 自回归的语言模型学习的目标是 ,而模仿学习的本质是在学习
我们将策略选择类比为“条件生成模型”,那么需要生成模型的建模工具就可以直接迁移到策略分布建模中,从而解决了“只能输出均值/单峰”的结构限制问题。
6.三类“表达性策略分布”
正如我在上文所提及的,网络表达能力和分布表达能力不同,为了解决这个问题,我们类比了生成模型的建模工具,这一章我会介绍三种方法来让输出分布能表达多峰/复杂结构。
- 高斯混合(Mixture of Gaussians, MoG) 用多个高斯分布的加权和表示策略分布: 网络输出的是 。MoG能显式表达多模态,是对单峰高斯的直接扩展;但在高维动作空间中, 很大或者方差结构复杂会导致网络参数爆炸、训练困难。并且推理时需要采样整个混合分布,计算成本较高。
- 离散化 + 自回归(Discretize + Autoregressive)
将连续动作按维度或按区间离散化,随后用自回归分解:
网络输出的一系列条件分布。自回归的优势在于可以表达复杂的依赖结构。然而缺点也是显而易见的,由于推理需要逐维生成,导致推理速度较慢。此外,离散化还会损失精度。
- 扩散策略(Diffusion Policy)
将行为动作生成写成逐步去噪过程:从噪声动作出发,通过 步迭代预测噪声或残差,最终得到动作样本。
7.模仿学习 Version 1:最大化对数似然
在引入表达性策略分布后,模仿学习的训练目标也随之发生变化。相比于Version 0中的 回归,Version 1将策略视为条件概率分布,并通过最大化专家动作在该分布下的对数概率进行训练:
这一目标允许策略在同一状态下为多种合理动作分配概率质量,而不是被迫输出一个折中的平均动作。从统计角度看,模型不再试图拟合条件期望,而是拟合完整的条件分布。
8. 表达性策略并不能解决所有问题
到目前为止,我们已经解决了模仿学习的第一个根本问题: 行为克隆中“学到均值动作”的失败,来源于对动作分布的错误建模假设,而非网络容量不足。通过引入更具表达能力的策略分布,并采用最大化对数似然的训练目标,Version 1 的模仿学习能够在离线示范数据上更忠实地复现专家行为。
然而,一个关键事实仍然没有改变:模仿学习依然是一个闭环决策问题。即便策略在示范数据上拟合得再好,其预测动作一旦被用于控制系统,仍然会影响后续状态的分布。这一点使得模仿学习与标准监督学习在结构上存在本质差异。
9. 模仿学习与监督学习的结构性差异
在标准监督学习中,输入变量的分布独立于模型的预测结果。模型输出不会反过来影响未来样本,因此逐点预测误差不会在时间维度上累积。
而在模仿学习中,情况完全不同。策略在时间步 的预测动作 会直接决定下一个状态 ,并进一步影响之后所有的输入分布。这意味着,即便在单步预测意义下误差很小,也可能通过系统动力学被不断放大。
因此,模仿学习的失败并非单纯来自“预测不准”,而是源于预测结果本身参与了数据生成过程。这是一个闭环系统特有的问题。
10. 分布不一致与误差累积
更形式化地看,模仿学习训练时所见到的状态分布来自专家轨迹,记为
而在部署时,系统实际访问到的状态分布由当前策略 (\pi) 所诱导,记为
只要策略存在任何预测误差,这两个分布就不可能完全一致。一旦策略偏离专家轨迹,系统就可能进入专家从未访问过的状态区域,而模型在这些区域缺乏监督信号,预测误差随时间不断放大。
这种现象通常被称为 covariate shift,在序列决策问题中则具体表现为 compounding errors(误差累积)。重要的是,这一问题即便在示范数据无限、模型表达能力足够强的理想条件下也无法完全避免。
11. 为什么“多收集示范数据”并不能根本解决问题
一个直觉性的想法是:如果误差来自于分布不一致,那么是否可以通过收集大量示范数据来覆盖更多状态?
课件明确指出,这一思路并不能从根本上解决问题。原因在于,失败往往发生在由模型自身错误诱导出的状态区域,而这些区域在专家示范中原本并不存在。即便示范数据规模极大,只要训练分布与执行分布存在系统性差异,误差累积就不可避免。
这表明:纯离线模仿学习在闭环系统中存在结构性风险。
12. DAgger:在策略访问的状态上引入监督
为缓解上述问题,DAgger(Dataset Aggregation)方法被提出。其核心思想可以概括为: 如果问题在于训练分布与执行分布不一致,那么就应当让训练分布逐步向执行分布靠拢。
DAgger 的做法是反复执行当前策略 ,并在策略实际访问到的状态 上查询专家动作 ,将这些新样本不断加入训练集,再重新训练策略。通过这一过程,训练数据的状态分布逐渐对齐 ,从而显著缓解误差累积问题。
从分布角度看,DAgger 并不是简单地“纠正错误动作”,而是在持续重塑训练数据的状态空间覆盖范围。
13. 在线干预的现实约束
尽管 DAgger 在理论上具有良好的性质,其实践应用仍然面临显著挑战。持续查询专家意味着算法必须在线运行,并且需要一个可以在任意状态下提供正确动作的专家接口。
在许多真实系统中,这样的专家并不总是可用,或者查询成本极高。因此,原始 DAgger 在工程上并不总是可行。
14. Human-Gated DAgger:更可行的干预范式
为降低专家干预成本,介绍了一种更贴近现实的变体,通常称为 Human-Gated DAgger。在这种设置下,策略默认自行控制系统;只有当专家判断策略即将发生严重错误时,才介入并提供纠正示范。
这种方法并未消除分布偏移问题,而是通过在高风险状态附近提供稀疏但关键的监督信号,对策略进行局部修正。实践表明,这种干预范式在机器人等复杂系统中更具可操作性。
15. 模仿学习在强化学习体系中的定位
综合来看,模仿学习提供了一种在低风险、低交互成本条件下获得可行策略的方式,尤其适合作为复杂强化学习系统的初始化手段。然而,它本身并不提供通过环境反馈持续改进策略的机制,也无法保证策略性能超越专家。
因此,在现代系统中,模仿学习通常被视为强化学习流程中的一个阶段,而非最终解决方案。
