Lecture 1 Introduction
0.引言
在传统的机器学习中,我们习惯于这样的设定
给定一组输入,以及对应的正确答案 让模型学习到一个函数
然而现实世界中,大量问题无法被这样简单建模。例如:机器人的连续决策或者语言模型的连续上下文对话。这些目标并没有标准答案。
因此强化学习解决的核心问题是:
当一个模型需要在时间序列中不断做决定、且当前状态的做的动作会影响未来的观察与结果时,我们怎么解决这个问题。
1.强化学习与监督学习的区别
监督学习的假设非常强:
- 数据是给定的
- 每一个样本都有正确的标签
- 模型只负责预测
强化学习不同于监督学习,强化学习不是仅仅学习给定数据的映射关系,而是通过交互获得奖励信号来调整决策,简而言之,强化学习是在学习行为。
- 模型需要自行做决定
- 决策的优劣由奖励模型评估
- 当前状态的决策会影响后续的数据分布
强化学习学习到的是一个策略:
上面这个式子的意思是:
在状态下,以某种概率决定动作
这里的行为可以是机器人控制关节,LLM进行的回复或者是agent进行的网页交互等等动作。
2.为什么要学习强化学习
由于现实世界的很多问题并没有足够的数据标签来支持传统的监督学习,正如刚才列举的机器人交互决策、大语言模型等。强化学习因此应运而生,机器人的行走、抓取和LLM的后训练等都是强化学习的广泛应用。
强化学习的一个关键直觉是:
智能体能否在通过反复尝试和反馈中,逐渐学会更好的行为。
3.如何将行为表示成数据?
四个基本要素
- 状态(State)
- 动作(Action)
- 观测(Observation)
- 奖励(Reward)
轨迹(Trajectory) 一个完整的交互过程被记录为一条轨迹:
也被称为rollout,长度可以是1,也可以很长。
4.State vs Observation:为什么要区分?
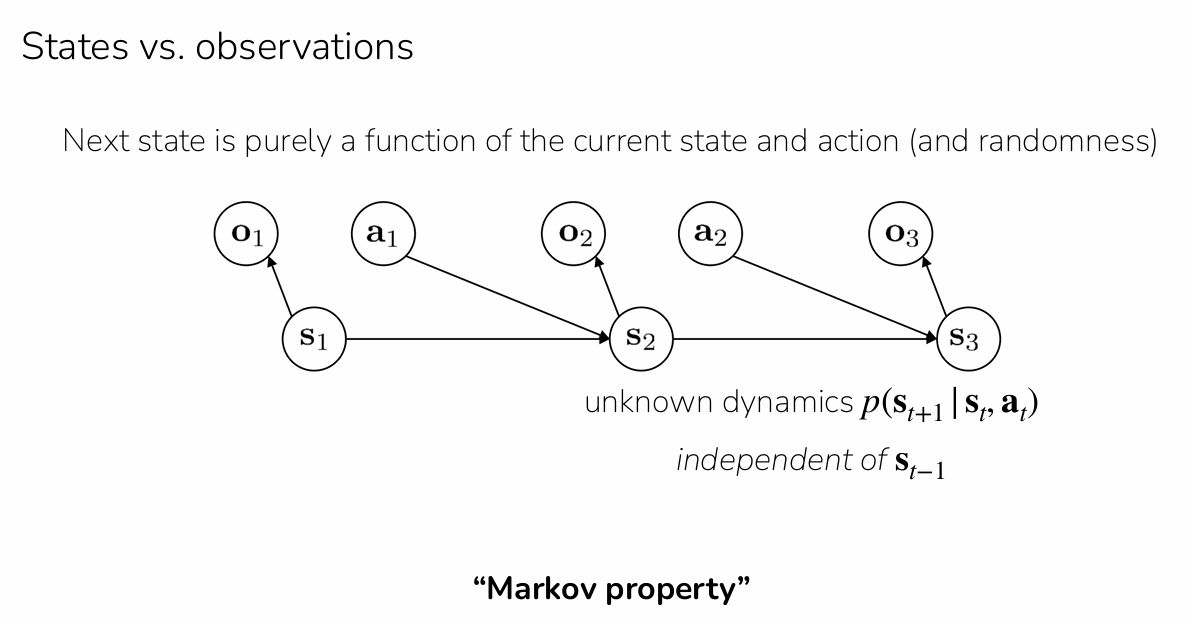 Markov假设: 如果时刻使用的是状态:
Markov假设: 如果时刻使用的是状态:
意思是:下一个状态仅仅依赖当前的状态和动作,与更早的历史无关。
这就是Markov Decision Process(MDP)。 然而现实系统中经常无法获取到完整状态,这时只能使用observation(),需要给策略记忆能力:
5.如何用神经网络表示“行为”?
策略可以用神经网络表示:
- 输入:状态()或观测()
- 输出:动作分布
- 参数:神经网络权重 一次交互流程:
- 观察当前状态
- 从策略()输出的动作分布中采样动作
- 环境转移到
- 重复上述操作 得到一条轨迹
6.强化学习真正的优化目标
表面上看,我们的优化目标是下面这个函数
是在状态下采取动作得到的即时奖励。
直观上看,这个式子的含义是希望从时间步 到 内,获得的总奖励尽可能大。
然而一个重要的问题是,这个奖励总和并不是一个确定值。由于环境是随机的,即使你采取了某个动作 ,下一个状态 可能不确定,由环境动态 决定。此外,策略本身也是随机的,策略 是一个概率分布,表示在状态 下选择不同动作的概率。所以即使策略固定,每次运行也可能选不同的动作。
因此,每条轨迹的总奖励都是随机变量,不能直接最大化一个随机值。
所以真正优化的是:期望回报
我们不再追求某一次跑出来的总奖励最大,而是希望所有可能轨迹的平均回报最大。
- :一条完整的轨迹,即
- :在参数为 的策略下,生成这条轨迹的概率。
- :对所有可能轨迹按其概率加权求期望。
这就是强化学习的核心优化目标:最大化期望回报。
其中:
这个公式描述了一条完整轨迹的概率是如何构成的:
- :初始状态的概率
- :在状态 下选择动作 的概率
- :环境转移概率
整个乘积表示:从初始状态开始,依次按照策略选动作,并根据环境动态转移状态,最终形成整条轨迹的概率。
因此我们得到了一个关键结论:在强化学习中,我们要优化的不是单次的累计奖励,而是策略产生的轨迹的期望累计奖励。
7.Value Function:衡量策略好不好
为了评估和改进策略,引入两个重要概念。
Value Function(值函数)
含义:从状态开始,按策略行动,未来能获得的期望总奖励。
Q Function(动作值函数)
含义:在状态下先执行动作,然后继续按策略,能获得的期望总奖励。
